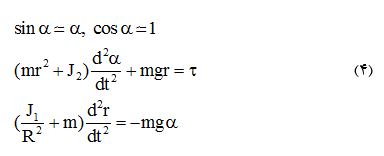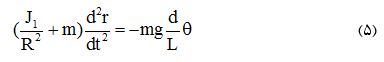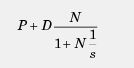مقدمه
سیستم گوی و میله یکی از بادوام ترین و مهمترین مدلهای آزمایشگاهی برای آموزش مهندسی سیستم های کنترل است. این سیستم به طور گسترده مورد استفاده قرار می گیرد که علت آن به خاطر تعداد زیادی از روشهای طراحی مدرن و کلاسیک است که می توانند بر اساس آن مورد مطالعه قرار بگیرند. سیستم گوی و میله بسیار ساده است که شامل یک گوی چرخان بر روی یک میله طولانی می باشد. زمانی که یک طرف میله ثابت باشد، طرف دیگر روی محور خروجی یک موتور الکتریکی قرار می گیرد و بنابراین میله می تواند بوسیله یک سیگنال کنترل الکتریکی به تقویت کننده موتور منحرف شود. موقعیت گوی می تواند با استفاده از یک سنسور مخصوص اندازه گیری شود. این سیستم یک خصوصیت بسیار مهم دارد و آن ناپایداری حلقه باز است زیرا خروجی سیستم بدون هیچ محدودیتی برای یک ورودی ثابت (زاویه میله) افزایش می یابد. کار کنترلی، تنظیم اتوماتیک موقعیت گوی با تغییر موقعیت موتور است. این یک کار مشکل است زیرا گوی در یک مکان روی میله نمی ماند زمانی که زاویه میله صفر نباشد؛ اما با شتابی حرکت می کند که متناسب با انحراف میله است. این سیستم را می توان به صورت خطی تقریب زد و با روش کنترل فیدبک خطی خروجی آن را تنظیم کرد. تحلیل پایداری این سیستم به کمک مدل فضای حالت یا تابع انتقال انجام می شود.
در این پروژه ضمن معرفی معادلات ریاضی حاکم بر ساختار و بدست آوردن تابع انتقال سیستم، عملکرد حلقه بسته آن با کنترل کننده PD و جبرانساز پیش فاز در محیط نرم افزاری متلب مورد بررسی و تجزیه و تحلیل قرار خواهد دادیم.
تعریف مسئله:
سیستم گوی و میله در شکل 1 نشان داده شده است. با اعمال زاویه θ می توان موقعیت یک سر میله را تعیین کرد. با فرض اینکه سر دیگه میله در جایی ثابت شده باشد، می توان موقعیت گوی بر روی میله را کنترل کرد. همانطور که مشخص است سیستم دارای دو درجه آزادی است که یکی زاویه میله و دیگری مکان گوی در روی میله است. هدف کنترل مکان گوی بر روی میله است. در این سیستم ورودی کنترل θ می باشد.
شکل 1) سیستم گوی و میله
فرضیات مسئله:
1) گوی بر روی میله حرکت غلتشی دارد.
2) رابطه بین جابجایی انتهای سمت راست میله و زاویه θ به صورت زیر تقریب زده شود.
مدل سازی سیستم:
در ابتدا، معادلات دیفرانسیل حاکم بر مسئله را به دست می آوریم. معادلات سیستم از روش لاگرانژ بر اساس تعادل انرژی در سیستم بدست می آید که به فرم زیر خواهند بود:
که در این معادله r فاصله مرکز گوی از انتهای ثابت میله، α زاویه میله نسبت به افق، τ گشتاور متحرک، m جرم گوی، J1 ممان اینرسی گوی و J2 ممان اینرسی میله است. این معادله غیرخطی است. برای تجزیه و تحلیل سیستم نیاز است معادلات خطی سازی شده سیستم حول نقطه تعادل را به دست آوریم. برای این کار فرض می کنیم زاویه آلفا کوچک باشد در این حالت توان دوم تغییرات زاویه نسبت به زمان که در فرمول (2) وجود دارد تقریباً صفر است. بنابراین می توان بیان کرد که:
از طرفی رابطه زاویه آلفا را از (1) داریم پس می توان رابطه دوم از فرمول (3) را به صورت زیر بیان کرد:
حال برای بدست آوردن تابع تبدیل سیستم از طرفین رابطه (5) لاپلاس می گیریم:
شبیه سازی سیستم حلقه بسته گوی و میله با کنترل کننده PD
در این قسمت عملکرد سیستم حلقه بسته را در حضور کنترل کننده تناسبی – مشتقی مورد بررسی قرار می دهیم. برای این منظور از ابزار PID_Tuner برای تنظیم بهره های بلوک کنترل کننده PD آماده خود متلب استفاده می شود. فرمول کلی این کنترل کننده در بلوک متلب به صورت زیر است:
که P گین تناسبی و D گین مشتقی است. ضریب N نیز برای تنظیم بهتر قسمت مشتق گیر در نظر گرفته شده است. با کمک ابزار PID_Tuner که در پنجره اصلی بلوک کنترل کننده قرار دارد، می توان بهره های بهینه را که موجب عملکرد مطلوب سیستم می شوند، در حوزه زمان بدست آورد.
با توجه به داده های سیستم (که در گزارش کار پروژه آورده شده است)، تابع تبدیل حلقه باز سیستم برابر خواهد بود با:
با در نظر گرفتن این تابع، آن را در سیمولینک متلب مدل سازی می کنیم. سیستم حلقه بسته گوی و میله با مدل کنترل کننده PD در شکل 2 نمایش داده شده است.
شکل 2) کنترل سیستم حلقه بسته سیستم گوی و میله با کنترل کننده PD
مشخصه ورودی و خروجی این سیستم در شکل 3 ارائه شده است. همانطور که مشخص است، این کنترل کننده عملکرد پایدار و مطلوبی از سیستم حلقه بسته را ایجاد می کند.
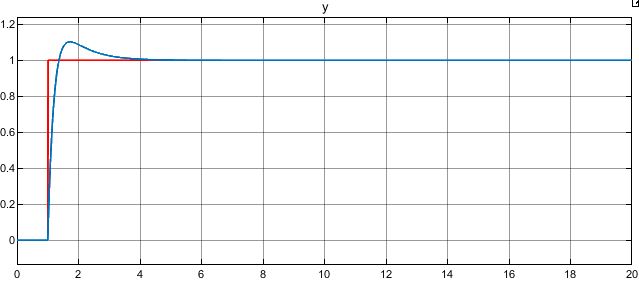
شکل 3) مشخصه ورودی و خروجی در حضور کنترل کننده PD
شبیه سازی سیستم حلقه بسته گوی و میله با جبران گر پیش فاز
در این قسمت به کمک جعبه ابزار sisotool کنترل سیستم را با جبرانساز پیش فاز در حوزه فرکانس مورد بررسی قرار می دهیم. برای اینکار از نمودارهای بود و نیکولز استفاده می کنیم. در اینجا معیار خود را حد فاز 45 درجه قرار داده و با تغییر صفر و قطب در نمودار نیکولز سعی می کنیم به این حد فاز دست یابیم. در نهایت مقدار گین و صفر و قطب تابع تبدیل بدست می آید. تابع تبدیل بعد از تنظیم به صورت زیر بدست می آید:
در ادامه نمودار بود و نیکولز سیستم با پارامترهای تنظیم شده در شکل 4 ارائه شده است. همانطور که ملاحظه می شود حلقه پایدار بوده و حد فاز 45 درجه است.
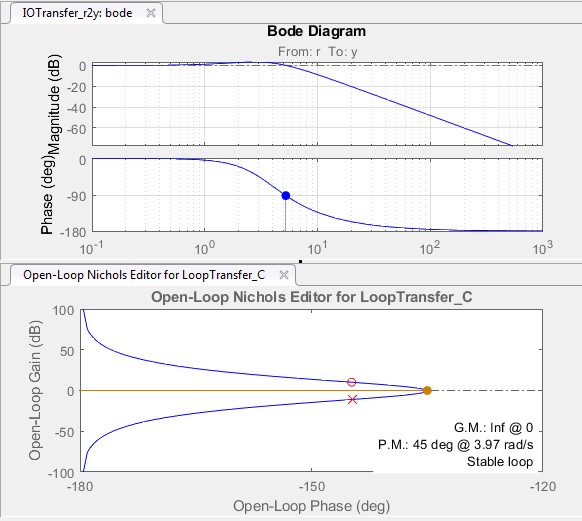
شکل 4) نمودار بود و نیکولز سیستم حلقه بسته گوی و میله با جبران ساز پیش فاز
حال تابع تبدیل جبران ساز طراحی شده را در نظر گرفته و آن را همراه با تابع تبدیل سیستم در فرم حلقه بسته قرار می دهیم. برای اینکار همانند کنترل کننده PD از مرحله قبل، از محیط سیمولینک متلب استفاده می کنیم. سیستم حلقه بسته با مدل جبران ساز پیش فاز در شکل 5 نمایش داده شده است.
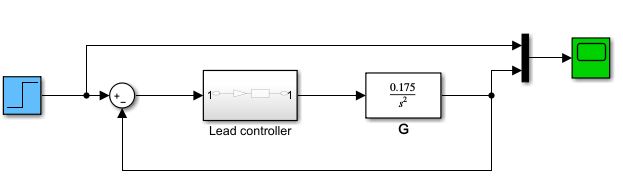
شکل 5) کنترل سیستم حلقه بسته گوی و میله با جبران ساز پیش فاز
مشخصه ورودی و خروجی این سیستم در شکل 6 ارائه شده است. همانطور که ملاحظه می شود مشخصه خروجی پایدار بوده و به سمت مقدار 1 میل می کند.
شکل 6) مشخصه ورودی و خروجی در حضور جبران ساز پیش فاز
از مقایسه نتایج مربوط به دو کنترل کننده PD و جبران ساز پیش فاز نتیجه می گیریم که هر دو روش در کنترل سیستم گوی و میله خوب عمل می کنند. در روش PD میزان بالازدگی در نمودار خروجی کمتر از روش دیگر است از طرفی در روش جبران ساز پیش فاز سیستم کمی زودتر به مقدار ماندگار خود می رسد.
———————————————————————————————————————————————————————–
توجه:
در این نوشتار در مورد سیستم گوی و میله مرسوم بحث کردیم و ضمن بیان معادلات ریاضی حاکم بر آن، کنترل سیستم حلقه بسته را در حضور دو کنترل کننده PD و جبران ساز پیش فاز مورد بررسی قرار دادیم. شما می توانید فایل های شبیه سازی به همراه گزارش کار 11 صفحه ای مربوط به شبیه سازی ها را – با جزئیات بیشتر – از لینک زیر خریداری کنید.
این پروژه جهت درک و فهم بهتر عملکرد این سیستم برای دانشجویان رشته برق – خصوصا گرایش کنترل – مناسب می باشد.
